نامساوی‌های ماتریسی خطی (Linear Matrix Inequality) و یا به طور خلاصه LMIs ابزاری بسیار قدرتمند در حل مسائل بهینه‌سازی و شبیه‌سازی سیستم‌های کنترل، مهندسی، ریاضیات ، علوم کامپیوتر و ... هستند بطوریکه در دهه‌های اخیر بدون استفاده از LMIها پرداختن به مسائل جدید در زمینه‌های اشاره شده امری بسیار دشوار و گاهی غیر ممکن است.

با توجه به اهمیت موضوع در این محصول سعی شده است تا با بیان ساده ضمن مرور تاریخچه شکل‌گیری LMIها و تعاریف بهینه‌سازی، به بررسی مفاهیم مختلف پرداخته و با مثالهایی ساده مراحل نصب Toolboxهای مورد نیاز در نرم افزار MATLAB و روش برنامه نویسی آنها توضیح داده شود.

تولباکس YALMIP یک ابزار بهینه‌سازی پیشرفته و قدرتمند برای نرم‌افزار متلب است که به کاربران این امکان را می‌دهد تا به راحتی مسائل مختلف بهینه‌سازی را مدلسازی و حل کنند. این ابزار انواع مسائل بهینه‌سازی از جمله LMIها، برنامه‌نویسی خطی، درجه دوم، عدد صحیح مختلط، ماتریسی و حتی بهینه‌سازی مقاوم و مجموع مربعات را پشتیبانی می‌کند و با تعداد زیادی از سالورهای قدرتمند مانند GUROBI، MOSEK و SeDuMi سازگار است. تولباکس YALMIP بیشتر در حوزه‌های تحقیقاتی و مهندسی کاربرد دارد و به دلیل سادگی و انعطاف‌پذیری بالا، یکی از ابزارهای محبوب در میان دانشجویان و محققان است.

تعاریف و اصطلاحات کاربردی

• بهینه‌سازی (Optimization): بهینه‌سازی ریاضی و یا به طور خلاصه بهینه‌سازی عبارت است از یافتن مناسب‌ترین المان از بین المان موجود با توجه به محدودیت‌های مسئله به طوری که خروجی سیستم بهینه‌ترین مقدار ممکن باشد. به عبارت ساده‌تر، مسئله بهینه‌سازی (Optimization Problem) عبارت است از یافتن مقداری از ورودی‌های مجاز با توجه به شروط مسئله که به ازای آن خروجی تابع (سیستم) مقدار ماکزیمم و یا مینیمم خود را اختیار کند.
• تابع هدف (Objective Function): تابع هدف عبارت است از رابطه‌ای که در حل مسئله بهینه‌سازی قرار است مقدار ماکزیمم یا مینیمم خود را پیدا کند.
• قیود مسئله (Constraints): قیود یا محدودیت‌های مسئله به شرایط یا الزاماتی گفته می‌شود که در حین حل مسئله باید برآورده شوند. به عبارت دیگر محدودیت‌ها شرایط و الزامات حل مسئله هستند. وجود شرایط و محدودیت‌های سخت‌گیرانه ممکن است منجر به عدم همگرایی مسئله و یافتن پاسخ بهینه شود.

• پاسخ بهینه (Optimal Solution): پاسخ بهینه عبارت است از مقادیری از ورودی‌های مجاز که سبب ماکزیمم یا مینیمم شدن تابع هدف می‌شوند. این مقادیر ممکن است بصورت بهینه محلی (در یک بازه مشخص) یا بهینه سراسری (در تمام دامنه تعریف) معرفی شوند.

  

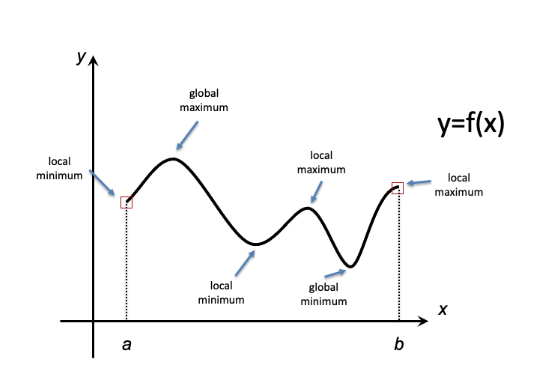
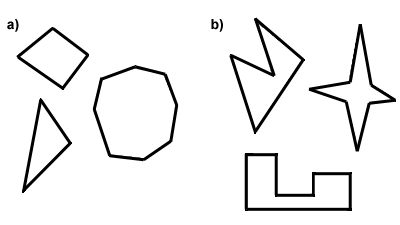
• ناحيه، مجموعه نقاط محدب (Convex Set): ناحيه محدب به ناحیه بسته‌ای اطلاق می‌شود که هرگاه دو نقطه ی دلخواه در آن انتخاب کنیم هر خط واصل این دو نقطه به طور کامل در ناحیه قرار گیرد. بدیهی است هر ناحیه ای که دارای سوراخ (حفره) باشد و یا نواحی هلالی شکل ناحیه ی غیر محدب (Non Convex or Concave) هستند. برای نمونه در شکل زیر اشکال a نواحی محدب و اشکال b نواحی غیرمحدب را نشان می‌دهند.

• فضای حل (Solution Space): فضای حل عبارت است از یک فضای یک، دو و یا چند بعدی که مسئله مجاز به انتخاب مقادیر مختلف از داخل این فضا است. به عبارت ساده‌تر فضای تعریف مسئله فضای حل نام دارد.
• سالور یا حل‌کننده (Solver): سالورها ابزارها و الگوریتم‌های محاسباتی هستند که فرایند حل یک مسئله بهینه‌سازی و جستجو در فضای حل را انجام می‌دهند.

محتویات این محصول شامل گزارشی جامع از تاریخچه و مفاهیم نامساوی‌های ماتریسی خطی و مراحل نصب و آموزش تولباکس YALMIP و سالورهای مورد نیاز برای حل این نامساوی‌ها در نرم‌افزار متلب می‌باشد.