بهینه‌سازی یکی از مهم‌ترین شاخه‌های ریاضیات کاربردی و علوم مهندسی محسوب می‌شود که هدف آن یافتن بهترین راه‌حل ممکن برای مسائل پیچیده است. در دنیای امروز که منابع محدود هستند و تقاضا برای بهره‌وری بالا روز به روز افزایش می‌یابد، اهمیت بهینه‌سازی بیش از پیش احساس می‌شود. این علم به ما کمک می‌کند تا با کمترین هزینه، حداکثر بازده را کسب کرده و از منابع موجود بهترین استفاده را ببریم.

بهینه‌سازی در واقع فرآیندی سیستماتیک است که در آن سعی می‌شود یک یا چند معیار را تحت شرایط و محدودیت‌های مشخص، به بهترین حالت ممکن برسانیم. این فرآیند نه تنها در علوم ریاضی و مهندسی کاربرد دارد، بلکه در زندگی روزمره نیز به طور طبیعی از آن استفاده می‌شود.

مفهوم و اصول بهینه‌سازی

بهینه‌سازی را می‌توان به عنوان فرآیند یافتن بهترین راه‌حل در میان تمام راه‌حل‌های ممکن تعریف کرد. در تعریف ریاضی، بهینه‌سازی به دنبال حداقل یا حداکثر کردن یک تابع هدف تحت مجموعه‌ای از قیدها و محدودیت‌هاست. این تابع هدف معمولاً نشان‌دهنده کمیتی است که می‌خواهیم آن را بهبود بخشیم، مانند سود، کیفیت، سرعت یا کارایی. 

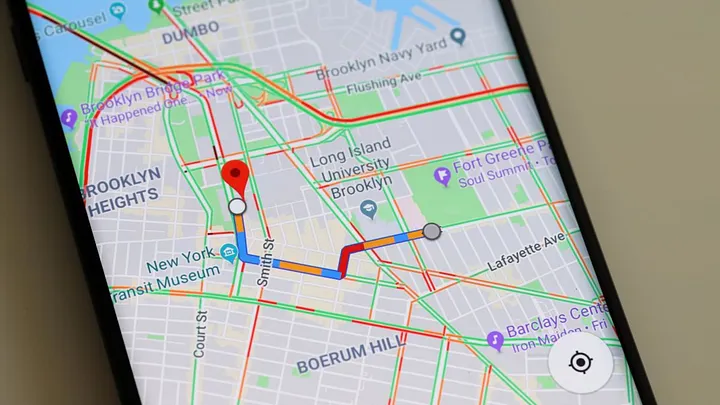
یک مثال ساده و روزمره از بهینه‌سازی، انتخاب کوتاه‌ترین مسیر برای رسیدن به محل کار است. در این مسئله، هدف اصلی کمینه کردن (Minimize) زمان سفر است. برای رسیدن به این هدف، چندین گزینه (یا متغیر تصمیم‌گیری) پیش رو داریم، مانند مسیر A که از بزرگراه می‌گذرد، مسیر B که از خیابان‌های اصلی می‌گذرد، یا مسیر C که کوتاه‌تر اما پرترافیک‌تر است. با این حال، این انتخاب با محدودیت‌هایی همراه است؛ برای مثال، مسیر انتخابی باید از خیابان‌های اصلی باشد زیرا رانندگی در کوچه‌های باریک مجاز نیست (محدودیت قانونی)، و همچنین باید مسیری را انتخاب کنیم که سوخت مصرفی آن از حد معینی کمتر باشد زیرا بنزین کافی در اختیار نداریم (محدودیت منابع). در انتها، پس از در نظر گرفتن تمام این شرایط و شاید حتی چک کردن برنامه‌ای مانند Google Maps برای دیدن ترافیک زنده، بهترین مسیر (راه‌حل بهینه) را انتخاب می‌کنیم که زمان سفر را با توجه به تمام این قیدها به حداقل برساند.

هر مسئله بهینه‌سازی دارای سه عنصر کلیدی است: متغیرهای تصمیم (Decision variables) که نشان‌دهنده پارامترهایی هستند که می‌توانیم آنها را کنترل کنیم، تابع هدف (Objective function) که معیار ارزیابی عملکرد سیستم محسوب می‌شود، و قیدها و محدودیت‌هایی (Constraints) که حدود مجاز برای متغیرهای تصمیم را مشخص می‌کنند. تعامل میان این سه عنصر، پیچیدگی و ماهیت هر مسئله بهینه‌سازی را تعیین می‌کند. برای نمونه در مثال بالا مسیرهای موجود متغیرهای تصمیم‌گیری،‌ محدودیت‌های موجود قیدهای مسئله و انتخاب کوتاه‌ترین مسیر تابع هدف مسئله است.

از دیدگاه‌های مختلف مسائل بهینه‌سازی را می‌توان به انواع مختلفی تقسیم‌بندی کرد. برای نمونه:

• بر اساس ماهیت تابع هدف و قیدها، مسائل به دو دسته خطی و غیرخطی تقسیم می‌شوند. مسائل خطی دارای ساختار ساده‌تر و روش‌های حل مشخص‌تری هستند، در حالی که مسائل غیرخطی پیچیدگی بیشتری دارند.
• همچنین بر اساس تعداد اهداف، مسائل به تک‌هدفه و چندهدفه تقسیم می‌شوند که هر کدام نیازمند رویکردهای متفاوتی هستند.
• در ادامه بر اساس تعداد سطح مسئله می‌توان مسائل را به تک سطحی یا چندسطحی تقسیم کرد. مسائل چندسطحی پیچیده‌تر هستند.
• و ...

کاربردهای بهینه‌سازی

کاربردهای بهینه‌سازی در عصر حاضر به قدری گسترده است که تقریباً در تمام جنبه‌های زندگی و فعالیت‌های اقتصادی آن را می‌توان مشاهده کرد. در صنایع تولیدی، بهینه‌سازی برای بهبود فرآیندهای تولید، کاهش هزینه‌های تولید، بهینه‌سازی زنجیره تأمین و مدیریت موجودی استفاده می‌شود. شرکت‌ها با استفاده از این تکنیک‌ها می‌توانند حداکثر بهره‌وری را با حداقل مصرف منابع به دست آورند. 

در حوزه حمل‌ونقل و لجستیک، بهینه‌سازی نقش حیاتی در تعیین مسیرهای بهینه، برنامه‌ریزی ترافیک شهری، و مدیریت ناوگان حمل‌ونقل ایفا می‌کند. سیستم‌های ناوبری مدرن مانند GPS از الگوریتم‌های بهینه‌سازی برای یافتن کوتاه‌ترین یا سریع‌ترین مسیر استفاده می‌کنند. در صنعت هوانوردی نیز، برنامه‌ریزی پروازها، تخصیص هواپیماها به مسیرهای مختلف و بهینه‌سازی مصرف سوخت از جمله کاربردهای مهم این علم محسوب می‌شوند. 

بخش مالی و اقتصادی نیز بهره‌مند مهمی از بهینه‌سازی است. مدیریت پورتفولیو سرمایه‌گذاری، ارزیابی ریسک، قیمت‌گذاری اوراق بهادار و برنامه‌ریزی بودجه از جمله کاربردهای کلیدی در این حوزه هستند. بانک‌ها و مؤسسات مالی از تکنیک‌های بهینه‌سازی برای حداکثر کردن سود و حداقل کردن ریسک استفاده می‌کنند. 

در عصر دیجیتال، فناوری اطلاعات و هوش مصنوعی بیشترین سهم را از کاربردهای بهینه‌سازی دارند. یادگیری ماشین، شبکه‌های عصبی، پردازش تصویر، بهینه‌سازی موتورهای جستجو و طراحی الگوریتم‌ها همگی بر مبنای اصول بهینه‌سازی استوار هستند. حتی در طراحی وب‌سایت‌ها و کاربردهای موبایل نیز برای بهبود تجربه کاربری و عملکرد سیستم از این تکنیک‌ها استفاده می‌شود.

روش‌ها و تکنیک‌های بهینه‌سازی

پس از مدلسازی درست یک مسئله بهینه‌سازی نوبت به حل آن می‌رسد. روش‌های حل مسائل بهینه‌سازی را می‌توان به دو دسته کلی روش‌های کلاسیک و مدرن تقسیم کرد. در مسائل بزرگ و پیچیده حل مدل‌ها با استفاده از ابزارها و نرم‌افزارهای پیشرفته انجام می‌شود.

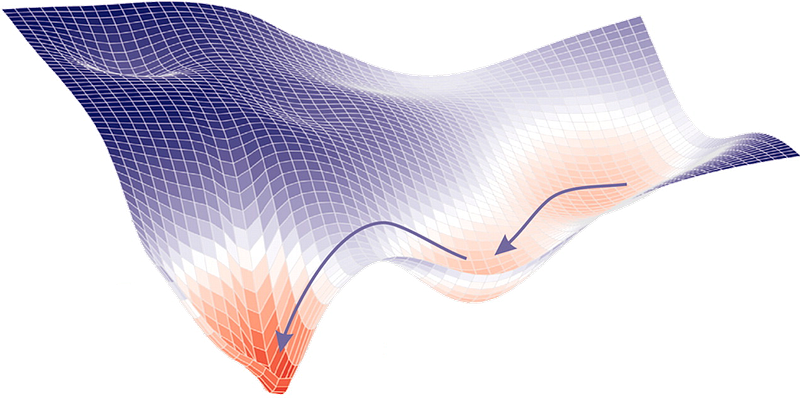
روش‌های کلاسیک بر پایه محاسبات ریاضی دقیق (Exact) استوار هستند و شامل تکنیک‌هایی مانند روش گرادیان، نیوتن-رافسون، لاگرانژ و روش‌های برنامه‌ریزی خطی می‌شوند. این روش‌ها برای مسائل با ساختار مشخص و نسبتاً ساده کارایی بالایی دارند و معمولاً به جواب دقیق می‌رسند. روش گرادیان یکی از پایه‌ای‌ترین تکنیک‌های بهینه‌سازی است که بر اساس مشتق تابع هدف عمل می‌کند و در جهت تندترین کاهش یا افزایش نرخ تابع هدف حرکت می‌کند. روش نیوتن-رافسون نیز با استفاده از مشتق مرتبه دوم، سرعت همگرایی بهتری ارائه می‌دهد.

در مقابل، روش‌های مدرن یا فراابتکاری از الهام طبیعت و رفتار موجودات زنده برای حل مسائل پیچیده استفاده می‌کنند. الگوریتم ژنتیک از فرآیند تکامل و انتخاب طبیعی الهام گرفته و برای مسائل پیچیده با فضای جستجوی بزرگ مناسب است. الگوریتم ازدحام ذرات از رفتار دسته‌جمعی پرندگان و ماهی‌ها الهام گرفته و در یافتن نقاط بهینه عملکرد خوبی دارد. الگوریتم شبیه‌سازی تبرید از فرآیند سرد شدن فلزات در طبیعت الهام گرفته و قابلیت فرار از نقاط بهینه محلی را دارد. الگوریتم‌های مورچگان نیز از رفتار مورچه‌ها در یافتن کوتاه‌ترین مسیر به منابع غذایی الهام گرفته‌اند. این روش‌ها اگرچه همیشه به جواب دقیق نمی‌رسند، اما برای مسائل پیچیده و غیرخطی نتایج قابل قبولی ارائه می‌دهند. 

انتخاب روش مناسب بهینه‌سازی بستگی به عوامل مختلفی دارد از جمله نوع مسئله، اندازه آن، دقت مورد نیاز، زمان در دسترس و منابع محاسباتی موجود. برای مسائل ساده و خطی، روش‌های کلاسیک معمولاً بهترین انتخاب هستند، در حالی که برای مسائل پیچیده و غیرخطی، روش‌های فراابتکاری عملکرد بهتری دارند.

چالش‌ها و محدودیت‌ها

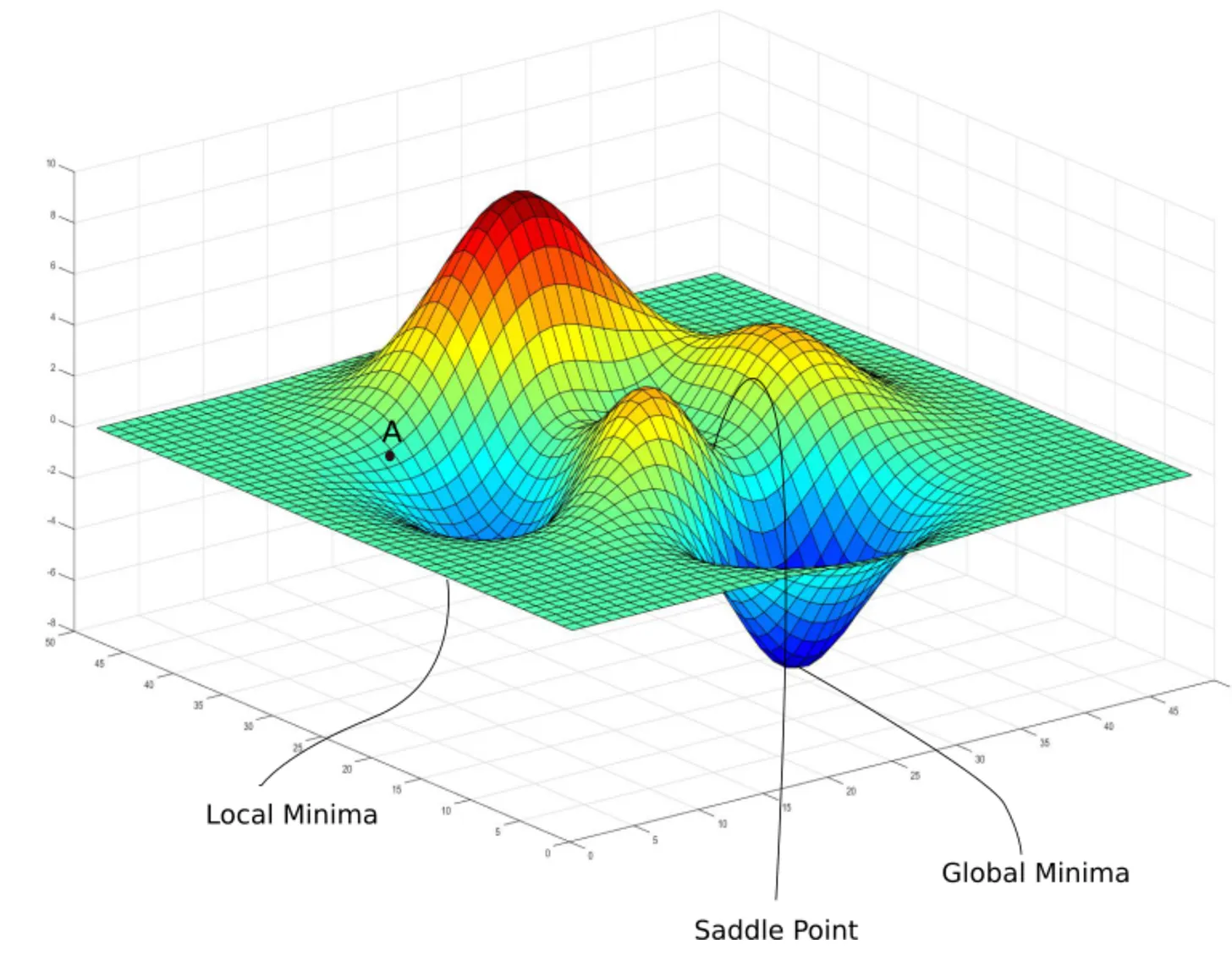
علی‌رغم پیشرفت‌های چشمگیر در حوزه بهینه‌سازی، هنوز چالش‌ها و محدودیت‌های مهمی وجود دارد که محققان و مهندسان با آن‌ها دست و پنجه نرم می‌کنند. یکی از اصلی‌ترین چالش‌ها، پیچیدگی محاسباتی مسائل است. برخی از مسائل بهینه‌سازی در دسته مسائل NP-Hard قرار می‌گیرند که حل دقیق آن‌ها در زمان معقول تقریباً غیرممکن است. این موضوع باعث می‌شود که محققان مجبور به استفاده از روش‌های تقریبی و ابتکاری باشند. 

مسائل چندهدفه نیز یکی دیگر از چالش‌های مهم محسوب می‌شوند و تصمیم‌گیرندگان با اهداف متعدد و گاهی متضاد مواجه هستند. برای مثال، در طراحی یک محصول ممکن است بخواهیم همزمان کیفیت را حداکثر و هزینه را حداقل کنیم که این دو هدف معمولاً در تضاد با یکدیگر قرار دارند. حل این گونه مسائل نیازمند تکنیک‌های خاصی مانند پارتو-بهینگی است. 

عدم قطعیت و وجود نویز در داده‌ها از دیگر مشکلات عملی است که دقت و قابلیت اعتماد نتایج بهینه‌سازی را تحت تأثیر قرار می‌دهد. در دنیای واقعی، داده‌ها اغلب دارای خطا، ناقص یا در حال تغییر هستند که این موضوع حل مسائل بهینه‌سازی را پیچیده‌تر می‌کند. برای مقابله با این مشکل، تکنیک‌های بهینه‌سازی تحت عدم قطعیت و بهینه‌سازی مقاوم توسعه یافته‌اند. 

محدودیت‌های محاسباتی نیز از جمله موانع عملی هستند. برخی از مسائل بهینه‌سازی نیازمند قدرت محاسباتی بسیار بالا و زمان زیادی برای حل هستند که این موضوع استفاده از آن‌ها را در کاربردهای زمان-حساس محدود می‌کند. همچنین، مدل‌سازی نادرست مسائل می‌تواند به نتایج غیرواقعی و غیرکاربردی منجر شود.

نتیجه‌گیری و چشم‌انداز آینده

بهینه‌سازی امروزه به یکی از ضروری‌ترین ابزارها در علم و صنعت تبدیل شده است که نقش کلیدی در بهبود عملکرد سیستم‌ها، کاهش هزینه‌ها و افزایش بهره‌وری ایفا می‌کند. از طراحی هواپیماهای مدرن گرفته تا بهینه‌سازی ترافیک شهری، از مدیریت منابع انرژی تا توسعه داروهای جدید، همه و همه مدیون پیشرفت‌های این علم هستند. 

آینده بهینه‌سازی با پیشرفت‌های تکنولوژی گره خورده است. محاسبات ابری و پردازش موازی امکان حل مسائل پیچیده‌تر و بزرگ‌تر را فراهم می‌کنند. هوش مصنوعی و یادگیری ماشین نیز راه‌های جدیدی برای بهینه‌سازی خودکار و تطبیقی ایجاد کرده‌اند. الگوریتم‌های یادگیری تقویتی قادر هستند در محیط‌های پویا به طور خودکار استراتژی‌های بهینه‌سازی را یاد بگیرند و بهبود بخشند. محاسبات کوانتومی نیز پتانسیل انقلابی در حوزه بهینه‌سازی دارد و ممکن است بتواند مسائلی را حل کند که امروزه غیرممکن به نظر می‌رسند. بهینه‌سازی چندهدفه، بهینه‌سازی تحت عدم قطعیت و بهینه‌سازی در زمان واقعی از جمله حوزه‌هایی هستند که انتظار می‌رود در آینده نزدیک شاهد پیشرفت‌های قابل توجهی در آن‌ها باشیم.

در انتها باید اشاره کرد که بهینه‌سازی نه تنها ابزاری برای حل مسائل فنی است، بلکه روش تفکری است که ما را به سمت یافتن بهترین راه‌حل‌ها در تمام جنبه‌های زندگی هدایت می‌کند. درک اصول و کاربردهای این علم، برای هر کسی که در دنیای مدرن فعالیت می‌کند، ضروری به نظر می‌رسد.